유진의 코딩스토리
Python DL 실습 3 [오차역전파] 본문


Affine 계산 그래프
입력값에 가중치를 곱하고 bias를 더해 계산하는 층
은닉층이 2개인 경우 계산 과정 : affine층 → sigmoid층 → affine층 → sigmoid층 → affine층 → softmax층
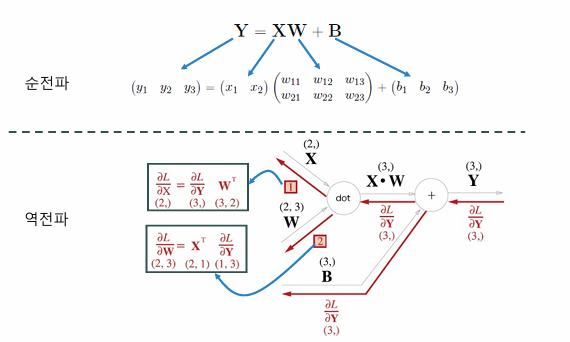
add layer는 그대로 가져옴
loss값의 미분을 구하려면
역전파 방식으로 속도가 빨라짐

Sigmoid 역전파 그래프
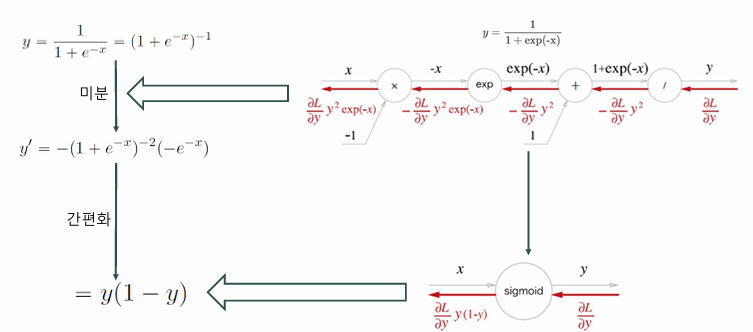
역전파를 과정에서 활성화함수인 sigmoid를 거칠 때 sigmoid의 미분값은 y(1-y)로 간편화할 수 있다.
이로 인해 역전파 계산과정이 간편해진다.
Sigmoid 활성화 함수의 문제와 대안
기울기 소실 문제(Gradient Vanish)
은닉층의 깊이가 깊어질수록 역전파 과정에서 학습을 진행할수록 기울기가 작아지는 현상
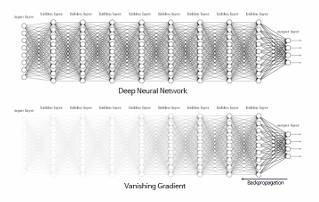
기울기는 활성화 함수의 미분값을 포함하는데 이 값이 1보다 작은 경우 층이 지날 때마다 기울기가 소실된다.
원인과 대안
sigmoid함수와 tanh함수는 S자형 곡선을 지닌 활성화함수로 입력값이 커지거나 작아질수록 출력값이 0에 가까워지므로 미분값이 0에 근접하게 된다. 이로 인해 역전파 과정에서 학습을 진행할수록 기울기가 거의 전달되지 않는다.
이에 대한 대안으로는 Relu함수가 사용되는데 relu함수의 경우 0보다 작은 값은 0으로 만들고 그 외의 값은 기울기가 1로 유지되는 비선형 함수이다. 기울기가 1로 유지되는 특성으로 인해 기울기 소실문제에 덜 민감하다.


Relu 함수의 미분
역전파 과정 시 활성화 함수의 미분값이 필요하므로 Relu함수의 미분값을 구해보자.



오차역전파법 구현하기
학습 알고리즘 4단계

TwoLayerNet클래스 구현
# TwoLayerNet 클래스 구현
import os ,sys
current_dir = os.path.dirname(__file__)
parent_dir = os.path.dirname(current_dir)
sys.path.append(parent_dir)
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
# 계층 생성
self.layers = OrderedDict()
self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
self.layers['Relu1'] = Relu()
self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
self.lastLayer = SoftmaxWithLoss()
# 순전파로 신경망 출력을 계산하는 함수
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
# 신경망 출력과 정답을 비교해서 손실값을 계산하는 함수
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return self.lastLayer.forward(y, t)
# 실제 예측을 했을 때 정답을 맞췄는지 정확도를 계산
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
if t.ndim != 1 : t = np.argmax(t, axis=1)
accuracy = np.sum(y == t) / float(x.shape[0])
return accuracy
# 수치 미분으로 가중치를 계산하는 함수
def numerical_gradient(self, x, t):
loss_W = lambda W: self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads
# 역전파 방식으로 가중치를 업데이트 하는 함수
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.lastLayer.backward(dout) # 손실값 미분함수로 기울기를 구하는 부분
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout) # 각 Layer의 가중치 기울기를 구하는 부분
# 역전파 방식으로 구한 가중치를 저장하는 부분
grads = {}
grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
위 TwoLayerNet 클래스를 불러와 Mnist 숫자 데이터를 인식하고 정확도 검증해보자.
# MNIST 숫자 데이터를 인식하고 검증
import os, sys
print(os.getcwd())
current_dir = os.path.dirname(os.getcwd())
print(current_dir)
os.chdir(current_dir)
# sys.path.append(parent_dir)
# import torch
import numpy as np
from dataset.mnist import load_mnist
from ch04.two_layer_net import TwoLayerNet
# 데이터 읽기
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
# 신경망 생성
network = TwoLayerNet(input_size=784, hidden_size=80, output_size=10)
iters_num = 20000 # 학습 횟수
train_size = x_train.shape[0]
batch_size = 200 # 배치 크기 100개로 지정
learning_rate = 0.1 # 학습률
train_loss_list = []
train_acc_list = []
test_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
for i in range(iters_num):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
# grad = network.numerical_gradient(x_batch, t_batch) # 수치 미분 방식
grad = network.gradient(x_batch, t_batch) # 오차역전파법 방식(훨씬 빠름)
# 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
loss = network.loss(x_batch, t_batch) # 손실값의 history를 저장
train_loss_list.append(loss)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print(train_acc, test_acc)'Azure 실습 > Azure deep learnig' 카테고리의 다른 글
| OpenCV 실습 (0) | 2024.10.29 |
|---|---|
| Python DL 실습 5 [합성곱 신경망] (0) | 2024.10.25 |
| Python DL 실습 4 [학습 관련 기술] (0) | 2024.10.25 |
| Python DL 실습 2 [신경망학습] (0) | 2024.10.23 |
| Python DL 실습 1 [퍼셉트론, 신경망] (0) | 2024.10.23 |




